Bitcoinový slovník naučný

Jak by řekl poručík Aldo Raine – počítání s reálnými čísly přináší spoustu úskalí. Prvním z nich je to, že musíte počítat s reálnými čísly. Nad nekonečnou množinou reálných čísel sice můžeme kreslit krásně ladné křivky, ale počítat se v tom nikomu nechce. Mnohem lepší situace by však mohla být nad nějakou konečnou množinou třeba celých čísel. Když se k této konečné množině definují dvě binární operace (třeba sčítání + a násobení ×), a celé to splňuje níže uvedené podmínky, tak se tomu říká konečné těleso.

V tělese F musí platit:

• Asociativita sčítání: a + (b + c) = (a + b) + c pro libovolné a, b, c ∈ F
• Komutativita sčítání: a + b = b + a pro libovolné a, b ∈ F
• Existence nulového prvku: existuje 0 ∈ F takové, že pro všechna a ∈ F platí a + 0 = 0 + a = a
• Existence opačného prvku: pro všechna a ∈ F existuje −a ∈ F takové, že platí a + (−a) = (−a) + a = 0
• Asociativita násobení: a × (b × c) = (a × b) × c pro všechna a, b, c ∈ F
• Komutativita násobení: a × b = b × a pro všechna a, b ∈ F
• Existence jednotkového prvku: existuje 1 ∈ F takové, že pro všechna a ∈ F platí 1 × a = a × 1 = a
• Existence inverzního prvku: pro všechna a ≠ 0 existuje a⁻¹ ∈ F takové, že platí a × a⁻¹ = a⁻¹ × a = 1
• Distributivita: a × (b + c) = a × b + a × c pro všechna a, b, ∈ F
• Netrivialita: 0 ≠ 1

Není to žádná raketová věda. Jedná se vesměs o obvyklé vlastnosti sčítání a násobení. Pokud by někomu chybělo odčítání a dělení, představí si místo nich přičítání opačného prvku, resp. násobení inverzním prvkem. Aby nám uvedené podmínky platily i v konečném tělese (tj. tělese s konečným počtem prvků), musí být počet prvků prvočíslo. Toto prvočíslo se také nazývá charakteristika tělesa. Schválně si zkuste vyrobit těleso o dvanácti prvcích a uplatněte výše uvedená pravidla. Nebude to fungovat.

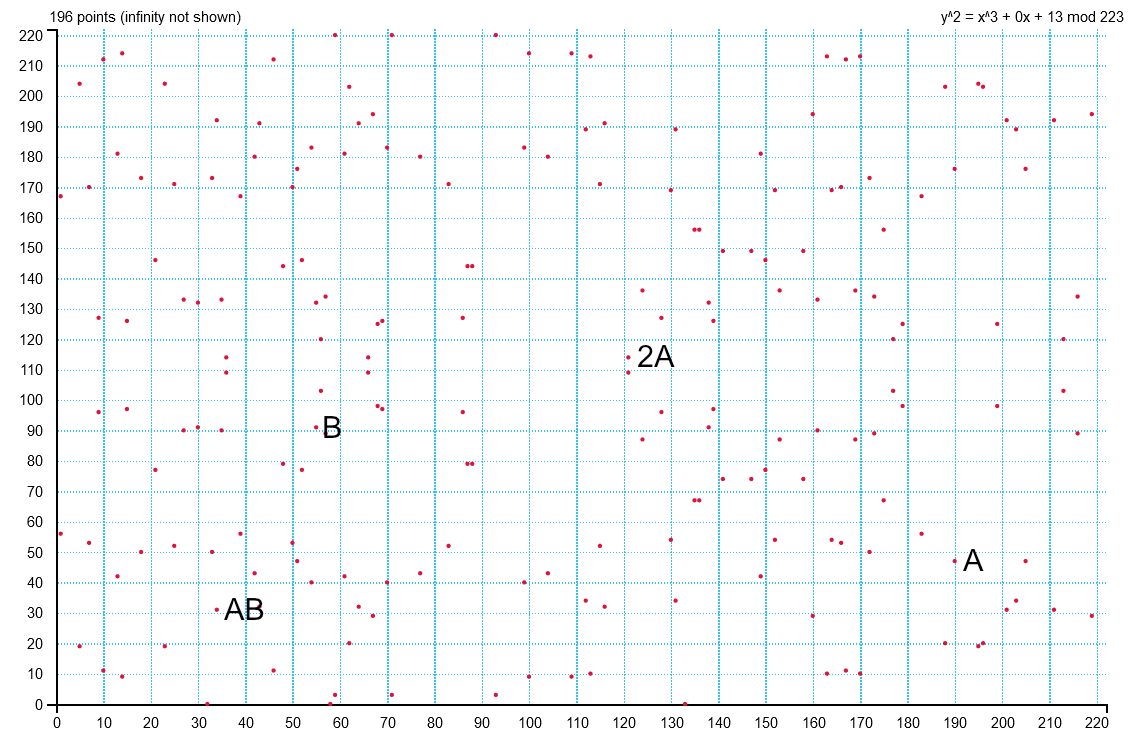
Pokud bychom si chtěli v tělese GF(223) cvičně vypočíst bod křivky y² = x³ + 13 pro x = 190, budeme počítat nejprve na pravé straně:

190³ + 13 mod 223 = 6859013 mod 223 = 202

Abychom nyní odmocnili y² = 202, ověříme si nejprve, že charakteristika p našeho tělesa GF(p) modulo 4 vyjde 3. To znamená, že (p + 1) mod 4 = 0, tedy že lze (p + 1) beze zbytku dělit 4. V tom případě můžeme použít k odmocnění následující hack – podle Malé Fermatovy věty a^p−1 mod p = 1. To znamená, že:

a² = a² × 1 = a² × a^p−1 = a^p+1

Protože p je prvočíslo, tedy liché, můžeme (p+1) dělit dvěma a tedy provést i následující techtle mechtle:

a = a^(p+1)÷2

Řekněme, že a² = b, pak

a = a^(p+1)÷2 = a^2(p+1)÷4 = (a²)^(p+1)÷4 = b^(p+1)÷4

Nic si z toho nedělejte, já to taky pobral teprve asi až na pátý pokus. Až to budete mít, můžeme jít odmocňovat:

y² = 202

y = 202^(223+1)÷4 mod 223
y = 202⁵⁶ mod 223
y = 1257988552198402112716025241425554802066116810455891304419632544898614527285976320036463847342459011535449669236965185786568769536 mod 223

y = 47

Začínalo to být zajímavé… Naštěstí jsme v konečném tělese a nezapomněli jsme na modulo (v praxi se s ním pracuje již v průběhu mocnění, vizte kupříkladu zde). Bod křivky A[190, 47] je též vyznačen na grafu výše. Jen pro pořádek zmiňme, že pro x = 190 vyhovuje i bod opačný k A tj. A'[190, 176] (223 − 47 = 176). Než si zkusíme nějaké ty body sečíst, podíváme se, jak by sčítání vypadalo graficky v množině reálných čísel. Tam stačí sestrojit přímku procházející dvěma sčítanými body P, Q, která nám (téměř vždy) protne křivku právě v ještě jednom dalším bodě R. Obraz bodu R v osové souměrnosti podle osy x je součtem bodů P, Q.

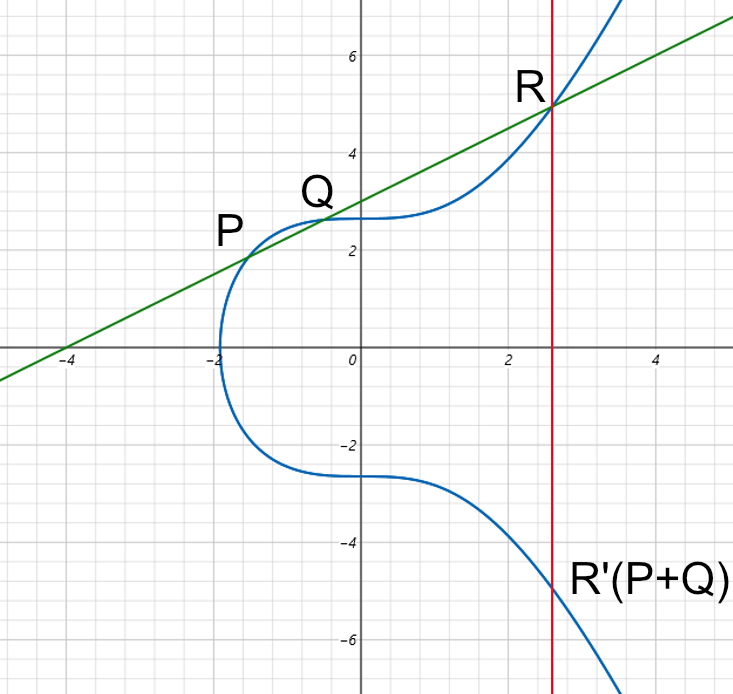
Přestože v „tělesovém“ grafu nám rýsování přímek již nebude fungovat, algebraicky to bude vypadat v obou případech stejně:

Směrnice přímky procházející sčítanými body bude
λ = (y₂ − y₁) ÷ (x₂ − x₁)
Rovnice přímky je
y = λx + κ
Dosazením do rovnice eliptické křivky najdeme x‐ovou souřadnici průniku přímky s danou křivkou (tj. x₃)
0 = x³ − (λx + κ)² + ax + b
přičemž koeficient u x² je roven −λ² = −(x₁+x₂+x₃) (Viètovy vzorce pro kořeny); odtud
x₃ = λ² − x₁ − x₂
y‐ová souřadnice průniku přímky s křivkou (tedy −y₃) je −y₃ = λx₃ + κ; odtud
y₃ = λ(x₁ − x₃) − y₁

Dosadíme‐li do rovnic náš „tělesový“ bod A[190, 47] a k němu třeba bod B[55, 91] jako druhý sčítanec, měl by nám vyjít bod AB[34, 31].

Speciální variantou sčítání bodů je pak sečtení bodu se sebou samým, ergo zdvojnásobení bodu. Graficky by tato operace vypadala jako tečna k eliptické křivce ve sčítaném bodě, která nám opět protne křivku ještě v jednom dalším bodě. Výsledný bod je opět obrazem v osové souměrnosti podle x. V algebraické formě to pak bude vypadat takto:

Směrnicí tečny je derivace křivky
λ = (3x² + a) ÷ 2y
Výsledné body pak budou
x₂ = λ² − 2x₁
y₂ = λ(x₁ − x₂) − y₁

Zdvojnásobení bodu A[190, 47] by mělo vyjít jako bod 2A[121, 114]. Opětovným zdvojnásobením bodu 2A získáme bod 3A[1,167], přičemž x opakování zdvojnásobování můžeme nazývat jako násobení skalárem – celým číslem x, které představuje počet opakování zdvojnásobení bodu.

Nesmíme zapomenout na případ, ve kterém by přímka (ať už procházející dvěma různými sčítanýmí body, nebo tečna ve zdvojnásobovaném bodě) byla rovnoběžná s osou y. Pro tento případ definujeme výsledek takového součtu (zdvojnásobení) jako bod v nekonečnu. Označíme jako O ; pak libovolný bod křivce A + O = A (identické zobrazení).

Počet všech bodů ležících na křivce se pak nazývá řád křivky. Na našem cvičném tělese GF(223) je můžeme najít prostým dosazením všech variací x, y do rovnice křivky. Zjistíme, že #GF(223) = 196 (včetně nevlastního bodu v nekonečnu). Na větších tělesech už bychom museli použít nějaký pokročilejší algoritmus (Schoof‐Elkies‐Atkin), popř. musíme věřit specifikaci.

Prohlásíme‐li bod A za generátor a operaci sčítání bodů za grupovou operaci ∘, můžeme si vygenerovat cyklickou grupu řádu n. Řád grupy je dán počtem bodů (prvků grupy), které stihne generátor opakovaným zdvojnásobováním (sčítáním se sebou samým) vygenerovat, než vyjde (n × A = O).

Tak jako těleso, i (Abelova) grupa G má nějaká svá pravidla:

• Uzavřenost: a ∘ b ∈ G pro libovolné a, b ∈ G
• Asociativita: a ∘ (b ∘ c) = (a ∘ b) ∘ c pro libovolné a, b, c ∈ G
• Komutativita: a ∘ b = b ∘ a pro libovolné a, b ∈ G
• Existence neutrálního prvku: existuje O ∈ G takové, že pro všechna a ∈ G platí a ∘ O = O ∘ a = a
• Existence inverzního prvku: pro všechna a ∈ G existuje a⁻¹ ∈ G takové, že platí a ∘ a⁻¹ = a⁻¹ ∘ a = O

Jak již bylo naznačeno, opakování grupové operace představuje ve své podstatě mocnění, byť je v aditivní notaci zapisováno jako násobení (n je kladné celé číslo): \begin{array}{l} \ n\times A\ =\underbrace{A\ \circ \ A\ ...\ A\ \circ \ A}_{\ n}\\ \end{array} Totéž zapsáno v multiplikativní notaci: \begin{array}{l} \ A^{n}\ =\underbrace{A\ \circ \ A\ ...\ A\ \circ \ A}_{\ n}\\ \end{array} Poněvadž naše grupa bodů je aditivní (grupovou operací je sčítání bodů), držme se prvního zápisu a toto „mocnění“ nazývejme násobení bodu skalárem.

Na závěr si předvedeme efektivní implementaci násobení skalárem metodou double‐and‐add:

def nasobeni_skalarem(bod, skalar):
 n = skalar
 aktualni = bod
 vysledek = 0  # neutrální prvek / bod v nekonečnu
 while n:
  if n & 1:  # bitový součin
   vysledek += aktualni  # přičtení aktuálního bodu k výslednému
  aktualni += aktualni  # zdvojnásobení aktuálního bodu
  n >>= 1  # bitový posuv vpravo
 return vysledek

Můžeme pokračovat na anatomii bitcoinové křivky.